Punto Flotante

Por qué son necesarios los números de punto flotante

Como la memoria de los ordenadores es limitada, no puedes almacenar números con precisión infinita, no importa si usas fracciones binarias o decimales: en algún momento tienes que cortar. Pero ¿cuánta precisión se necesita? ¿Y dónde se necesita? ¿Cuántos dígitos enteros y cuántos fraccionarios?

  • Para un ingeniero construyendo una autopista, no importa si tiene 10 metros o 10.0001 metros de ancho ─ posiblemente ni siquiera sus mediciones eran así de precisas.
  • Para alguien diseñando un microchip, 0.0001 metros (la décima parte de un milímetro) es una diferencia enorme ─ pero nunca tendrá que manejar distancias mayores de 0.1 metros.
  • Un físico necesita usar la velocidad de la luz (más o menos 300000000) y la constante de gravitación universal (más o menos 0.0000000000667) juntas en el mismo cálculo.

Para satisfacer al ingeniero y al diseñador de circuitos integrados, el formato tiene que ser preciso para números de órdenes de magnitud muy diferentes. Sin embargo, solo se necesita precisión relativa. Para satisfacer al físico, debe ser posible hacer cálculos que involucren números de órdenes muy dispares.

Básicamente, tener un número fijo de dígitos enteros y fraccionarios no es útil ─ y la solución es un formato con un punto flotante.

Cómo funcionan los números de punto flotante

La idea es descomponer el número en dos partes:

  • Una mantisa (también llamada coeficiente o significando) que contiene los dígitos del número. Mantisas negativas representan números negativos.
  • Un exponente que indica dónde se coloca el punto decimal (o binario) en relación al inicio de la mantisa. Exponentes negativos representan números menores que uno.

Este formato cumple todos los requisitos:

  • Puede representar números de órdenes de magnitud enormemente dispares (limitado por la longitud del exponente).
  • Proporciona la misma precisión relativa para todos los órdenes (limitado por la longitud de la mantisa).
  • Permite cálculos entre magnitudes: multiplicar un número muy grande y uno muy pequeño conserva la precisión de ambos en el resultado.

Los números de coma flotante decimales normalmente se expresan en notación científica con un punto explícito siempre entre el primer y el segundo dígitos. El exponente o bien se escribe explícitamente incluyendo la base, o se usa una e para separarlo de la mantisa.

Mantisa Exponente Notación científica Valor en punto fijo
1.5 4 1.5 ⋅ 104 15000
-2.001 2 -2.001 ⋅ 102 -200.1
5 -3 5 ⋅ 10-3 0.005
6.667 -11 6.667e-11 0.0000000000667

El estándar

Casi todo el hardware y lenguajes de programación utilizan números de punto flotante en los mismos formatos binarios, que están definidos en el estándar IEEE 754. Los formatos más comunes son de 32 o 64 bits de longitud total:

Formato Bits totales Bits significativos Bits del exponente Número más pequeño Número más grande
Precisión sencilla 32 23 + 1 signo 8 ~1.2 ⋅ 10-38 ~3.4 ⋅ 1038
Precisión doble 64 52 + 1 signo 11 ~5.0 ⋅ 10-324 ~1.8 ⋅ 10308

Hay algunas pecularidades:

  • La secuencia de bits es primero el bit del signo, seguido del exponente y finalmente los bits significativos.
  • El exponente no tiene signo; en su lugar se le resta un desplazamiento (127 para sencilla y 1023 para doble precisión). Esto, junto con la secuencia de bits, permite que los números de punto flotante se puedan comparar y ordenar correctamente incluso cuando se interpretan como enteros.
  • Se asume que el bit más significativo de la mantisa es 1 y se omite, excepto para casos especiales.
  • Hay valores diferentes para cero positivo y cero negativo. Estos difieren en el bit del signo, mientras que todos los demás son 0. Deben ser considerados iguales aunque sus secuencias de bits sean diferentes.
  • Hay valores especiales no numéricos (NaN, «not a number» en inglés) en los que el exponente es todo unos y la mantisa no es todo ceros. Estos valores representan el resultado de algunas operaciones indefinidas (como multiplicar 0 por infinito, operaciones que involucren NaN, o casos específicos). Incluso valores NaN con idéntica secuencia de bits no deben ser considerados iguales.

Representación de los números en punto flotante

En un ordenador típico los números en punto flotante se representan de la manera descrita en el apartado anterior, pero con ciertas restricciones sobre el número de dígitos de q y m impuestas por la longitud de palabra disponible (es decir, el número de bits que se van a emplear para almacenar un número). Para ilustrar este punto, consideraremos un ordenador hipotético que denominaremos MARC-32 y que dispone de una longitud de palabra de 32 bits (muy similar a la de muchos ordenadores actuales). Para representar un número en punto flotante en el MARC-32, los bits se acomodan del siguiente modo: 

Signo del número real x: 1 bit
Signo del exponente m: 1 bit
Exponente (entero |m|): 7 bits
Mantisa (número real |q|): 23 bits

 En la mayoría de los cálculos en punto flotante las mantisas se normalizan, es decir, se toman de forma que el bit más significativo (el primer bit) sea siempre '1'. Por lo tanto, la mantisa q cumple siempre la ecuación (19).

Dado que la mantisa siempre se representa normalizada, el primer bit en q es siempre 1, por lo que no es necesario almacenarlo proporcionando un bit significativo adicional. Esta forma de almacenar un número en punto flotante se conoce con el nombre de técnica del 'bit fantasma'.

Se dice que un número real expresado como aparece en la ecuación (18) y que satisface la ecuación (19) tiene la forma de punto flotante normalizado. Si además puede representarse exactamente con |m| ocupando 7 bits y |q| ocupando 24 bits, entonces es un número de máquina en el MARC-323

La restricción de que |m| no requiera más de 7 bits significa que:

\begin{displaymath}\vert m\vert \leq (1111111)_{2} = 2^7 - 1 = 127\end{displaymath}

 

Ya que $2^{127} \approx 10^{38}$, la MARC-32 puede manejar números tan pequeños como 10-38 y tan grandes como 1038. Este no es un intervalo de valores suficientemente generoso, por lo que en muchos casos debemos recurrir a programas escritos en aritmética de doble precisión e incluso de precisión extendida.

Como q debe representarse empleando no más de 24 bits significa que nuestros números de máquina tienen una precisión limitada cercana a las siete cifras decimales, ya que el bit menos significativo de la mantisa representa unidades de $2^{-24} \approx 10^{-7}$. Por tanto, los números expresados mediante más de siete dígitos decimales serán objeto de aproximación cuando se almacenen en el ordenador.

Por ejemplo: 0.5 representado en punto flotante en el MARC-32 (longitud de palabra de 32 bits) se almacena en la memoria del siguiente modo:

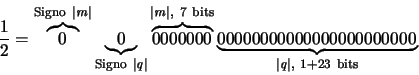
\begin{displaymath}\frac{1}{2} = \overbrace{0}^{\mathrm{Signo~\mathit{\vert m\ve......00000000000000000}_{\mathrm{\mathit{\vert q\vert},~1+23~bits}}\end{displaymath}

 

Ejemplo 5: Suponga un ordenador cuya notación de punto fijo consiste en palabras de longitud 32 bits repartidas del siguiente modo: 1 bit para el signo, 15 bits para la parte entera y 16 bits para la parte fraccionaria. Represente los números 26.32, $1.234 \cdot 10^{-4}$ y 12542.29301 en base 2 empleando esta notación de punto fijo y notación de punto flotante MARC-32 con 32 bits. Calcule el error de almacenamiento cometido en cada caso.

Solución: El número 26.32 en binario se escribe del siguiente modo:

\begin{displaymath}26.32_{10} = {11010.\overline{01010001111010111000}}_{2}\end{displaymath}

Empleando las representaciones comentadas, obtenemos:

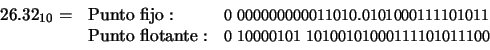
\begin{displaymath}\begin{array}{lll}26.32_{10} = & \mathrm{Punto~fijo:} &\m...... &\mbox{\small0 10000101 10100101000111101011100}\end{array}\end{displaymath}

Si expresamos el error como la diferencia entre el valor y el número realmente almacenado en el ordenador, obtenemos:

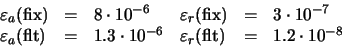
\begin{displaymath}\begin{array}{llllll}\varepsilon_{a}(\mathrm{fix}) & = & 8 ......arepsilon_{r}(\mathrm{flt}) & = & 1.2 \cdot 10^{-8}\end{array}\end{displaymath}

En cuanto a los otros dos números, obtenemos:

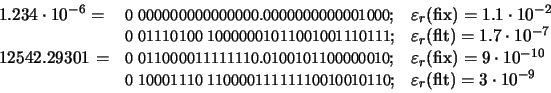
\begin{displaymath}\begin{array}{lll}1.234 \cdot 10^{-6} = & \mbox{\small0 000...... &\varepsilon_{r}(\mathrm{flt}) = 3 \cdot 10^{-9}\end{array}\end{displaymath}

 

Antes de entrar con detalle en la aritmética de los números en punto flotante, es interesante notar una propiedad de estos números de especial importancia en los cálculos numéricos y que hace referencia a su densidad en la línea real. Supongamos que p, el número de bits de la mantisa, sea 24. En el intervalo $\left[\frac{1}{2},1\right)$ (exponente f = 0) es posible representar 224 números igualmente espaciados y separados por una distancia 1/224. De modo análogo, en cualquier intervalo $\left[2^{f},2^{f+1}\right)$ hay 224 números equiespaciados, pero su densidad en este caso es 2f/224. Por ejemplo, entre 220 = 1048576 y 221 = 2097152 hay 224 = 16777216 números, pero el espaciado entre dos números sucesivos es de sólo $\frac{1}{16}$. De este hecho se deriva inmediatamente una regla práctica: cuando es necesario comparar dos números en punto flotante relativamente grandes, es siempre preferible comparar la diferencia relativa a la magnitud de los números. 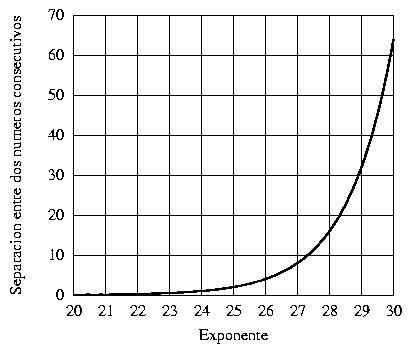En la figura (1) se representa gráficamente la separación entre dos números consecutivos en función del exponente f en el rango f = [20,30]. 
  
 

 Figura 1
Figure: Evolución de la separación entre dos números consecutivos en función del exponente, f, de la representación en punto flotante de un número real.
[bb=55 60 455 410, clip=true, scale=0.7]eps/expon